Representation Invariants

The abstraction function explains how information within the module is viewed abstractly by module clients. However, this is not all we need to know to ensure correctness of the implementation. Consider the size function in each of the two implementations. For ListSetNoDups, in which the lists of integers have no duplicates, the size is just the length of the list:

let size = List.length

But for ListSetDups, which allows duplicates, we need to be sure not to double-count duplicate elements:

let rec size = function
  | [] -> 0
  | h :: t -> size t + (if mem h t then 0 else 1)

How we know that we don't need to do this check in ListSetNoDups? Since the code does not explicitly say that there are no duplicates, implementers will not be able to reason locally about whether functions like size are implemented correctly.

The issue here is that in the ListSetNoDups representation, not all concrete data items represent abstract data items. That is, the domain of the abstraction function does not include all possible lists. There are some lists, such as [1; 1; 2], that contain duplicates and must never occur in the representation of a set in the ListSetNoDups implementation; the abstraction function is undefined on such lists. We need to include a second piece of information, the representation invariant (or rep invariant, or RI), to determine which concrete data items are valid representations of abstract data items. For sets represented as lists without duplicates, we write this as part of the comment together with the abstraction function:

module ListSetNoDups : Set = struct
  (** Abstraction function: the list [a1; ...; an] represents the set
      {a1, ..., an}.  [] represents the empty set.
      Representation invariant: the list contains no duplicates. *)
  type 'a set = 'a list
  ...

If we think about this issue in terms of the commutative diagram, we see that there is a crucial property that is necessary to ensure correctness: namely, that all concrete operations preserve the representation invariant. If this constraint is broken, functions such as size will not return the correct answer. The relationship between the representation invariant and the abstraction function is depicted in this figure:

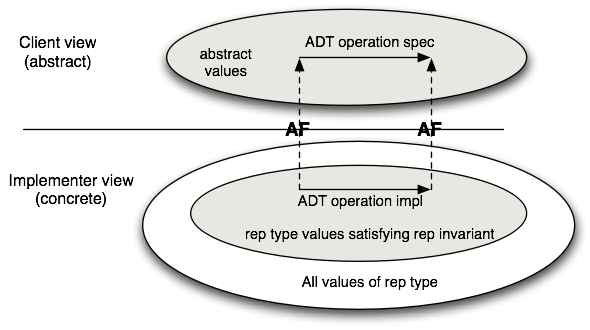
We can use the rep invariant and abstraction function to judge whether the implementation of a single operation is correct in isolation from the rest of the module. It is correct if, assuming that:

1. the function's preconditions hold of the argument values
2. the concrete representations of the arguments satisfy the rep invariant

we can show that

1. all new representation values created satisfy the rep invariant, and
2. the commutative diagram holds.

The rep invariant makes it easier to write code that is provably correct, because it means that we don't have to write code that works for all possible incoming concrete representations—only those that satisfy the rep invariant. For example, in the implementation ListSetNoDups, we do not care what the code does on lists that contain duplicate elements. However, we do need to be concerned that on return, we only produce values that satisfy the rep invariant. As suggested in the figure above, if the rep invariant holds for the input values, then it should hold for the output values, which is why we call it an invariant.