Abstraction Functions

The client of any Set implementation should not be able to distinguish it from any other implementation based on its functional behavior. As far as the client can tell, the operations act like operations on the mathematical ideal of a set. In the first implementation, the lists [3; 1], [1; 3], and [1; 1; 3] are distinguishable to the implementer, but not to the client. To the client, they all represent the abstract set {1, 3} and cannot be distinguished by any of the operations of the Set signature. From the point of view of the client, the abstract data type describes a set of abstract values and associated operations. The implementer knows that these abstract values are represented by concrete values that may contain additional information invisible from the client's view. This loss of information is described by the abstraction function, which is a mapping from the space of concrete values to the abstract space. The abstraction function for the implementation ListSetDups looks like this:

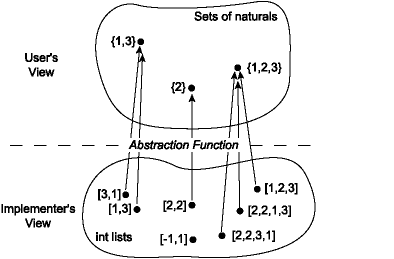
Notice that several concrete values may map to a single abstract value; that is, the abstraction function may be many-to-one. It is also possible that some concrete values do not map to any abstract value; the abstraction function may be partial. That is not the case with ListSetDups, but it might be with other implementations.

The abstraction function is important for deciding whether an implementation is correct, therefore it belongs as a comment in the implementation of any abstract data type. For example, in the ListSetDups module, we could document the abstraction function as follows:

module ListSetDups : Set = struct
  (* Abstraction function: the list [a1; ...; an] represents the
   * smallest set containing all the elements a1, ..., an.
   * The list may contain duplicates.
   * [] represents the empty set.
   *)
  type 'a set = 'a list
  ...

This comment explicitly points out that the list may contain duplicates, which is helpful as a reinforcement of the first sentence. Similarly, the case of an empty list is mentioned explicitly for clarity, although it is redundant.

The abstraction function for the second implementation, which does not allow duplicates, hints at an important difference: we can write the abstraction function for this second representation a bit more simply because we know that the elements are distinct.

module ListSetNoDups : Set = struct
  (* Abstraction function: the list [a1; ...; an] represents the set
   * {a1, ..., an}.  [] represents the empty set.
   *)
  type 'a set = 'a list
  ...