7.1 Hill-Climbing: Don't worry, be happy/optimistic: choose the best neighbor

From any given rearrangement, using a single swap produces a comparatively small set of additional candidate rearrangements. We think of these as neighbors that are reachable in one step. If you think about paths starting from the current candidate, including paths to the best solution, they all start off by taking a next step. The neighbors are exactly those next steps.

Recasting optimization in terms of paths and neighbors, we want to know how to pick a path --hopefully the shortest path, but we'll take what we can get-- that takes us to the best solution.

We have seen earlier that we cannot simply try out all paths. Therefore, we must somehow throw away some possibilities. One way to do that is to be optimistic and pick the path that looks ``best''. What might make a path look good? Well, if it takes us closer to a solution. Therefore, we might simply decide to look at all the neighbors, and pick the best one. Ties may be broken arbitrarily. If the current solution is better than all the neighbors, then we're done. Otherwise keep taking steps until improvements are marginal or some time limit is reached.

  

Figure 34: Training text, Plaintext, Encryption Key, and Ciphertext

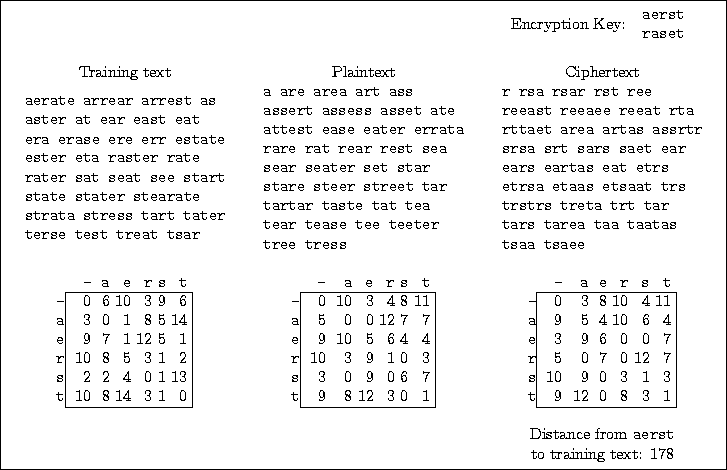
Let us now apply hill-climbing to an example a little bit bigger than in Section 6.1. Figure 34 shows the training text and plaintext that we use, plus the encryption key we use to generate the ciphertext.

Figures 35 through 38 show the steps that hill-climbing takes. Keep in mind that we are trying to make ciphertext frequencies match the frequencies of the training text -- pretend we don't know the plaintext and are trying to extract it by cracking the ciphertext. At each step, all the neighboring bigram tables are computed one at a time and their distances from the training frequencies computed. The one that is closest to training frequencies is chosen as the next table to continue searching from.

Figure 38 shows the final step, where we see that all neighbors of the table with labels ``raset'' are farther than it is from the training frequencies. This tells us the canonical (sorted top-line) encryption key is hopefully

aerst

raset

, and indeed it is! Thus, our hope that unscrambling frequencies would lead to cracking ciphertext is (probably) validated!

Observe that we looked at 44 keys, counting duplicates (we looked at 36 unique keys), which is better than looking at all 5!=120 keys. This again suggests that hill-climbing is effective in this situation at finding the best table, whereas exhaustive search would take much too long.

  

Figure 35: Hill-Climbing, Step 1: Go from aerst, 178 to aesrt, 144, marked ``*''.

  

Figure 36: Hill-Climbing, Step 2: Go from aesrt, 144 to arset, 106, marked ``*''.

  

Figure 37: Hill-Climbing, Step 3: Go from arset, 106 to table raset, 88, marked ``*''.

  

Figure 38: Hill-Climbing, Step 4: Stay at raset, 88 -- neighbors are worse.

Roadmap
Section 3.7	Encipher plaintext $\Rightarrow$ scramble frequencies.
Section 3.7	Decipher ciphertext $\Rightarrow$ unscramble frequencies.
Section 4.2	(Hope) Unscramble frequencies $\Rightarrow$ decipher ciphertext
Section 4.3	Unscramble = Bring ``close'' to intrinsic frequencies
	Approximate intrinsic frequencies with training text
	Assume ciphertext is medium to large so that unscrambled frequencies resemble intrinsic frequencies
Section 4.4	Use the L1 distance to measure ``closeness''; ignore labels.
Section 5.1	Sorting unigram frequencies does not work, but ``almost'' does.
	(Hope) When the frequency table for ciphertext matches the table for training text, read the encryption key off of the labels
Section 5.2	``Sort bigram frequencies'' is problematic.
Section 5.3	Exhaustive search is too slow; therefore, need an incomplete search.
Section 6.1	(Idea) Hill-Climbing: pick the best ``neighbor''
Section 6.2	Why swaps are so important, e.g. used to generate ``neighbors''
Section 6.3	The effect of swaps on bigram tables
Section 7.1	Hill-climbing and unscrambling frequencies appear to work
$(\rightarrow)$     Section 7.2	Hill-climbing in the abstract
Section 7.3	Improvement/alternative to hill-climbing