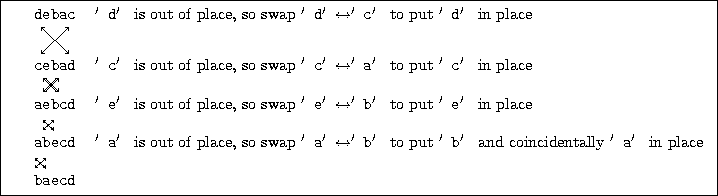6.2 Why Swaps Are so Important

We've tried to motivate the importance of swaps since Section 5.1, where our first decryption attempt involved sorting unigram frequencies: Most sorting algorithms are based on swaps. We saw swaps again when considering enumerating all keys for an exhaustive search, and yet again in our tentative exploration of hill-climbing. Why are swaps so important, e.g. why are they used for sorting? First of all, rearrangement or permutation is a fundamental operation in all of these areas:

• Sorting = rearranging elements in a list in order.
• Bottom line of a key = a rearrangement of the top line.
• Generating all keys = generating all rearrangements of the top line for use in the bottom line.

Now that we see that permutations are important, we also have the following fundamental fact:

• ``Transpositions, i.e. swaps, generate all permutations''.

That is, every permutation can be modified into every other permutation by a ``path'' or sequence of 0 or more swaps, e.g. no matter what key we start with, we can reach the decryption key using a sequence of 0 or more swaps.

The justification for this fundamental fact is simply that we can sort using swaps: As long as an item is out of order, swap it into place; repeat until done. (Selection sort does these swaps in a specific order, e.g. right-to-left.) For example, Figure 31 shows one way to get from "debac" to "baecd" using swaps.

  

Figure 31: Using Swaps to get from "debac" to "baecd"

So we know that we can always get from one permutation to another:

• Swaps can be used for sorting, because no matter what order the numbers are in, it is possible to swap them into sorted order.
• Our algorithm for generating all keys (permutations) will work because swaps generate all permutations.
• Our hill-climbing algorithm is not inherently prevented from reaching the decryption key: No matter what key we start with, there is a path of 0 or more swaps to the decryption key.¹⁰

Now that we understand why swaps are important, let us investigate them further: What effect do swaps have on bigram tables?

Roadmap
Section 3.7	Encipher plaintext $\Rightarrow$ scramble frequencies.
Section 3.7	Decipher ciphertext $\Rightarrow$ unscramble frequencies.
Section 4.2	(Hope) Unscramble frequencies $\Rightarrow$ decipher ciphertext
Section 4.3	Unscramble = Bring ``close'' to intrinsic frequencies
	Approximate intrinsic frequencies with training text
	Assume ciphertext is medium to large so that unscrambled frequencies resemble intrinsic frequencies
Section 4.4	Use the L1 distance to measure ``closeness''; ignore labels.
Section 5.1	Sorting unigram frequencies does not work, but ``almost'' does.
	(Hope) When the frequency table for ciphertext matches the table for training text, read the encryption key off of the labels
Section 5.2	``Sort bigram frequencies'' is problematic.
Section 5.3	Exhaustive search is too slow; therefore, need an incomplete search.
Section 6.2	Q: How do we perform an effective, incomplete search?
Section 6.1	(Idea) Hill-Climbing: pick the best ``neighbor''
Section 6.2	Why swaps are so important, e.g. used to generate ``neighbors''
$(\rightarrow)$     Section 6.3	The effect of swaps on bigram tables