4.4 Distance

We need a way of comparing two equal-sized tables for ``similarity'' or ``closeness''. Suppose you wish to compare the Genesis and Romeo and Juliet frequencies. As shown in Figure 21, a first step is to subtract the frequencies for each character.

  

Figure 21: Unigram Differences and Magnitudes of Differences

Since the sign (positive or negative) of the differences have nothing to do with how big the differences are, take the absolute value of each difference to get its magnitude. The last row shows the magnitude of each difference. (The differences do not quite jibe with the original frequencies because of rounding.)

The list of magnitudes gives us an idea of closeness, but it is cumbersome to deal with so much data. With bigrams, the tediousness would be even worse. Therefore, we would like to combine the magnitudes into a single number that measures the distance between two equal-sized tables. There are many possibilities of what function to use for distance, usually all based on the magnitudes of the differences between corresponding elements. For example,⁵

• Maximum or 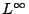$L^\infty$ distance: maximum magnitude
• L² distance: square root of the sum of the squares of the magnitudes
• Manhattan or taxicab or L¹ distance: sum of the magnitudes

For simplicity, choose the last one, the L¹ distance d. Why? It's simple and, as you will discover, tends to work. To compute d, pick two unigram or bigram tables with frequencies you wish to compare. Let N be the size of the character set, including a space. The values may contain either percentages or tallies, but both tables must have the same type of frequency! Take each absolute value of the difference between each element from the pair of tables and add all differences together:

$$\mbox{unigram distance } d =\sum_{j} \left\vert \mbox{\emph{f... ...m table1} - \mbox{\emph{freq}}_{i,j}^{\rm table2} \right\vert.$$

Your choice of table1 and table2 is irrelevant because of the absolute value. Index i ranges over all rows 1..N; index j ranges over all columns 1..N.

One question that we must answer is, what distances count as ``close''?