... key.¹

In many cryptosystems, the decryption key is ``easy'' to compute from the encryption key. Therefore, the encryption key must be hidden for the cryptosystem to be secure. However, there are some cryptosystems where it is (believed to be) infeasible to compute the decryption key from the encryption key, in which case it is OK for the encryption key to be public. So-called public key cryptosystems have this property, e.g. PGP/RSA.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...'q'.²

Why not always? Because of typos, abbreviations, words borrowed from other languages, and people in advertising that like to mess around with spelling.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... languages.³

See http://www.cs.wright.edu/people/faculty/fdgarber/740/ascii/ascii2freq.html for an example of frequencies in just words.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... frequencies.⁴

Ouvroir de Litterature Potentielle (``Potential Literature Workshop'') is a group about game-like methods of writing. Member Georges Perec wrote La Disparition without using the letter 'e'. The English translation, A Void, by Gilbert Adair also has no 'e'. Besides as a gimmick, Perec wrote without 'e' for plot/thematic reasons. Le Ton Beau De Marot: In Praise of the Music of Language, by Douglas R. Hofstadter, discusses both the original and the translation.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... example,⁵

These distances belong to the class of L^p (pronounced ``ell-pee'') norms: the pth root of the sum of the pth powers of the magnitudes. The limit as p goes to infinity is the 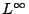$L^\infty$ norm.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... distances?⁶

When you do Project 7, you will discover that 70% does count as close. Although 70% does sound high, keep in mind that it is still relatively far away from the maximum possible distance of 200%.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... work.⁷

Actually, since different letters probably do have at least slightly different intrinsic unigram frequencies, if we have ``large enough'' training and ciphertexts, then their frequencies will converge to identical, intrinsic frequencies, in which case sorting unigram frequencies would work. The problem is, our experiments show that ``large enough'' appears to be on the order of multiple books or more.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... ciphertext.⁸

Conceptually, we have said to compute the table of bigram frequencies for each key by transforming ciphertext and then counting. We will see in Section 6.3 how we instead rearrange the frequencies in the original bigram table, thereby allowing us to omit the step of transforming ciphertext.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... frequencies.⁹

A human could visually inspect the hoped-for-plaintext and simply choose the one that is readable. However, without more complex algorithms that involve pattern recognition, a computer program has ``trouble'' visually inspecting text. Therefore, we stick to our idea of bringing the frequencies as close as possible to intrinsic frequencies.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... key.¹⁰

However, it is true that hill-climbing can get ``stuck'' at a local optimum, where all the ``local'' neighbors are farther away from training frequencies, so we will not reach the global optimum, the solution that is closest overall to training frequencies.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.