Lecture notes by
Lynette I. Millett
Revised by Michael Frei
If the CA is compromised, however, there is obviously a problem. The private key for the CA should therefore be kept in a very safe place. Fortunately, unlike the KDC for secret key cryptography, the CA does not need to be online all the time. The CA has two functions: certify bindings (i.e. certification) and store the certificates. Once created, the certificates can be stored anywhere and can even be procured (once signed) from an untrusted source.
What happens if a principal's private key is compromised? (In fact, in some cases it may be to an individual's benefit to suggest that a private key was compromised.) Once a principal's private key is compromised, then all the certificates associated with that principal will cause the wrong public key to be used. A solution is to insist that certificates have expiration dates. This limits damage but doesn't completely eliminate it. (Note that the KDC could have dealt with this problem just by deleting the KDC entry. Our problem with the CA is a direct consequence of not having the CA on-line all the time.)
We need a scheme to assert that a certificate that has not yet expired is no longer valid. A solution is to assign a unique serial number to each certificate and maintain a certificate revocation list (CRL). A certificate is of the form: {principal name, public key, serial number, expiration date}CA and a CRL is of the form {time of issue, revoked serial number, revoked serial number, . . .}CA. A certificate is considered invalid if the expiration date has expired or the serial number of the certificate appears on a recent CRL. It is tempting to use the time of the message to compare to the expiration date, but this is a bad idea. An attacker that knows a compromised private key can use whatever time needed when creating a message (e.g. send a message that was sent "yesterday"). It is also important to use the most current CRL possible.
Note that the existence of CRLs requires that the CA or some other source of CRLs be online. Without access to a recent CRL, there is no way to know whether to trust a given certificate. There are also some engineering tradeoffs that arise when using CRLs. For instance, if the expiration time is small (not too far in the future), then certificates will be constantly reissued and lots of traffic will be generated. Large expiration times lead to long CRLs. If CRLs are issued frequently, then the amount of time vulnerable to compromise is short but lots of network traffic is generated. If the CRLs are issued infrequently, then the possibility of compromise increases.
Having a single CA is unrealistic. There is no one entity that is trusted by everyone for everything (even in real life). Moreover, performance will not scale well. A solution is to have multiple CAs. The issue now becomes: how does a principal in one CA's domain get a public key for a principal in a different CA's domain? Imagine there is a user A in the CIA domain. Call the certifying authority CA-CIA. Similarly, imagine there is a user B in the KGB domain and CA-KGB is the CA. How can A communicate with B? A needs to know how to determine that a certification encrypted under CA-KGB's private key is valid. Thus A needs the public key of CA-KGB. A receives {CA-KGB, PCA-KGB}CA-CIA from CA-CIA. It then receives {B, PB}CA-KGB from CA-KGB. If A trusts both CA-CIA and CA-KGB then A must conclude that PB is B's public key.
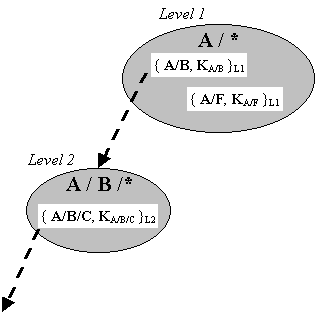
But what should lead Alice to believe that she can trust CA-KGB? One solution is to have an agreed mapping from principal names to the name of the CA that is considered an authority on those names. For example, one might go to the "cs" CA for names like fbs/cs and go to the "cornell" CA for names like cs/cornell, etc. See the figure below for an example of this hierarchy.

principal said statement
However, just because you say something doesn't make it true. Suppose
fbs said "the sun will rise today". Principal fbs has no control
over whether or not the sun will rise, so such a statement means nothing.
If fbs says "we will have a quiz in class today", however, then we
have reason to believe that there will be a quiz, because we have this
notion of authorities which looks likes the following (where
-> is a meta-logical operator used to separate the
hypotheses from the conclusion of
an inference rule):
P controls S, P said S -> S is true.
When authorities make a statement about that which they are an authority
of, we consider it as true. For example, we could have an authority
on names and public key bindings (name <-> Kname):
CA-A is an authority on A/*, or CA-A/B is an authority on
A/B/*
In a distributed system, what principals say can be altered
in transit. If we have a message m that is signed by some
principal's private key, {m}ka, then we know
that KA said m (notice: we're now thinking of
principals as either a person or a key, because whoever has that
key can say it)
We allow principals to speak for other principals. If P speaks for Q, then (P said m) implies (Q said m). Whatever P said can be regarded as having been said by Q. Stated as one of our rules,
P speaks for Q, P said m -> Q
said m.
So, we can have a Certificate Authority speak for another principal.
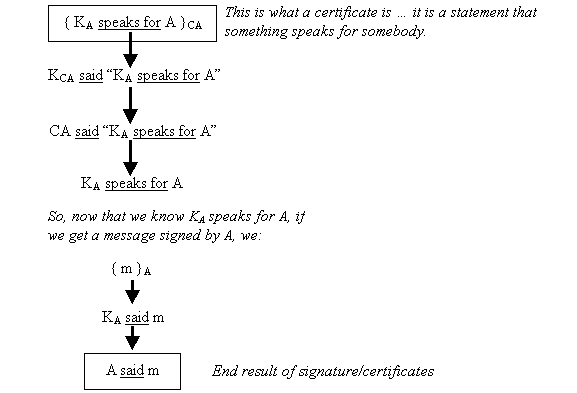
Now let's try to apply these formal definitions to the behavior
of certificates and Certificate Authorities. In the figure below, we
show how obtaining the certificate for A {A, KA}CA
can enable the authentication of a message sent from A. We will use
a simple single CA with KCA.
In the first version, names are hierarchical (e.g. A/B/C/D). An e-mail address such as fbs@cs.cornell.edu is represented as edu/cornell/cs/fbs. (In such a scheme, it easy to add a new name uniquely.) The PEM proposal is to have a CA for each subtree of the namespace. That is, a CA named A/B/C is responsible for all names of the from A/B/C/* (where * is a wildcard.) A CA named A/B is responsible for all names of the form A/B/*. A rule for certificates is that the issuer of a certificate must be a prefix of the principal's name in the certificate. That is, CA A/B can issue a certificate for A/B/C/D. Consider the following scenario
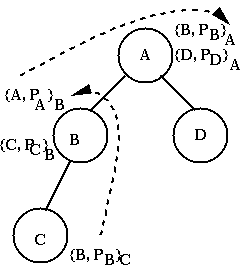
A can sign the public key of B, while B can certify the public key of A and of C.
A problem with the above scheme is that the CA at the root is too sensitive. Compromising A's private key in the above example would compromise everything below A. A new scheme was therefore proposed. The root is the Internet Policy Registration Authority (IPRA) and there are three classes of PCAs (Policy Certificate Authorities) below the IPRA. The PCAs sign things. The rule is that there is only one path in the hierarchy to any principal. It is easy to find the path, and therefore easy to acquire the necessary certificates. There are three classes of PCAs:
PGP asks each user to assign a "trust rating" to each public key that is on the user's public key ring. There are two parameters: valid -- the user believes that the key is associated with whom the user was told it is associated with, and trust -- a measure of how much the user trusts the principal as a signer. The trust parameter is three-valued: none, partial, and complete. If a certificate is signed by a principal the user completely trusts, then that key is valid. If a certificate is signed by two partially trusted users, then again the key is valid. Clearly, it is possible to devise very intricate trust management/key validity schemes. This area is not well-understood at this time. What are good properties for inferring trust? Should trust necessarily be transitive? Should trust be monotonic (once trusted, always trusted)?
Keys are generated in PGP as follows: 1.) the user specifies the size of the key (in bits) and then 2.) the user types a pass phrase. This pass phrase is then run through an MD5 cryptographic hash to obtain an IDEA key. The "private key" of the user is computed from the random timing in some typing that the user does. The private key is then encrypted locally with the IDEA key that was generated. Note: having the private key always encrypted implies that if the computer was stolen, the private key is still secure.