Secret Key Cryptography & DES

Lecturer: Professor Fred B. Schneider

Lecture notes by Lynette I. Millett

Last time we discussed several primitive cryptosystems. We mentioned two properties, confusion and diffusion, that are desirable in any cryptosystem.

There are three classes of cryptographic functions that turn out to be useful:

Secret Key Cryptography

Secret key cryptography involves two functions: These functions are inverses of each other, so that message = D(key, E(key, message)). The E and D notation is a bit verbose, so we will use the notation k{m} to say that message m was encrypted under key k.

Uses for secret key cryptography include: transmitting secret messages in the presence of passive eavesdroppers, storing information in encrypted form on insecure media, and authentication (determining who is involved in a given dialogue.) Note: if you are using encryption to store data on insecure media, most editors work on a decrypted form of data. Thus, they may store temporary unencrypted versions of your data.

Authentication, as we have seen it before, is often done with a password. However, that form of authentication involves revealing the 'secret' (password) in order to prove one's identity. We are interested in strong authentication--providing proof of identity without revealing the secret. In other words, strong authentication involves proving knowledge of a secret (key/password) without revealing the secret itself.

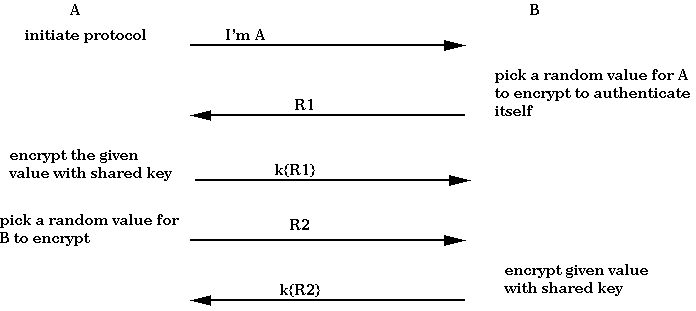
Suppose we would like user A to prove to user B that A is A without revealing the secret that is the essence of being A, and vice versa. Thus, we desire a protocol that allows A and B to authenticate themselves to each other. Assume that there is a shared, secret key: k. Knowing k is proof of being either A or B. The desired mutual authentication protocol works as outlined below. The arrows indicate sending a message.

There are many subtle errors that can arise when designing cryptographic protocols. We now illustrate some. First, note in the above protocol that B sends A two messages in a row. An obvious optimization might be to combine those messages into one, as well as having A announce itself and send a random bit string for B to encrypt at the same time.
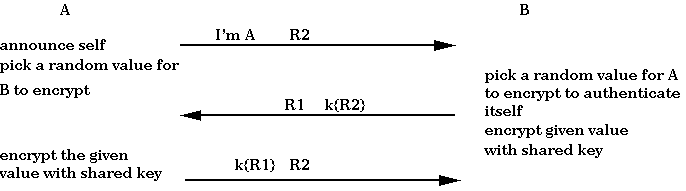This protocol, however, if flawed. In particular, it is susceptible to what is known as a reflection attack. It is possible for an eavesdropper, T, to convince B that T is A. T exploits the fact that B seems willing to encrypt challenges. Therefore, T can pretend to be A as follows:
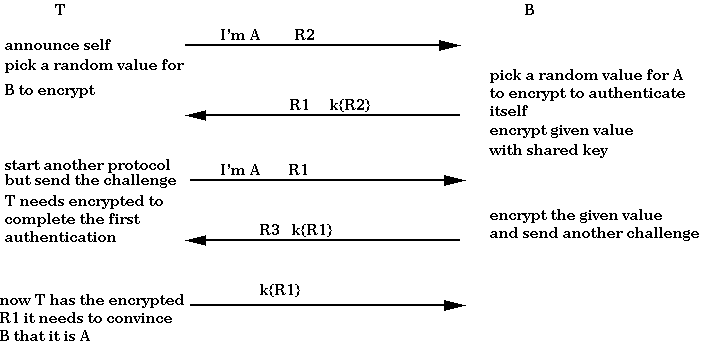After B sends R1 to T, T needs to get it encrypted under k in order to convince B that T is A. T therefore starts another session, sending R1 which B then returns encrypted. T now learns the encrypted version of R1 and can convince B that B is communicating with A.

There are several possible approaches to repairing the protocol:

Industrial-Strength Cipher: DES

Data Encryption Standard (DES) is an example of an industrial-strength encryption algorithm. The mathematics of why this results in a good cipher is beyond the scope of this course. However, we will discuss some details of how it works. DES is based on the IBM "Lucifer" algorithm of 1974 and became a U.S. standard in 1976. Having an encryption standard is useful, because it makes interactions possible that might otherwise need to be customized. The downside, of course, is the uncertainty as to whether there are agencies that can break the standard.

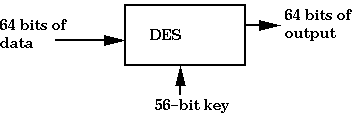
DES takes in 64 bits of data, a 56-bit key and executes 16 cycles of substitution and permutation before outputting 64 bits of data.

Is a 56-bit key long enough? This depends. Suppose you have a 50 MIP CPU. It can handle 300 kilobytes/second if DES is implemented in software. Due to expected increases in processor price/performance, it is necessary to add 1 bit to the key every 2 years to preserve this level of work for cracking DES. In 1993, Weinen at Bell Northern Research proposed a DES cracking machine. It uses a chip that costs $10.50 to manufacture and can try 50 million DES keys per second. Thus,

Note that DES encrypts only 64 bits at a time. How are long messages encrypted? There are two modes available that we will discuss: Electronic Code Book (ECB) and Cipher Block Chaining (CBC).

In ECB mode, a message is broken into 64 bit blocks and each block is encrypted separately. One problem with this approach is that if two blocks are identical, then they will be identically encrypted. Another problem is that a substitution attack is now possible. Rather than reading a message, an attacker can change the meaning of a message by snipping out pieces of the text and replacing them with encrypted versions of another message.

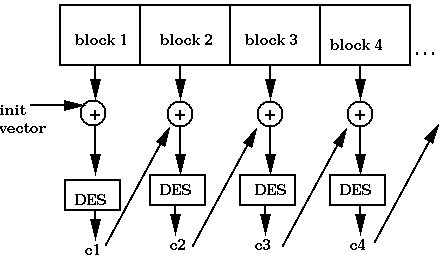
In CBC mode, "random" bits are added to each block based on the previous block. Specifically, each block is encrypted separately using not only the key but a random bit string as well. This bit string becomes part of the key material. The first block is XORed with an initialization vector. The result is then encrypted by DES as usual. This becomes the first ciphertext block. Also, this block is XORed with the second block, and then the result is encrypted by DES to become the second ciphertext block. The process continues as illustrated in the following diagram.

It is best to use a random initialization vector (even though it must then be included somewhere in the message). One could just use a vector of 0s as the initialization vector, but then an eavesdropper could detect identical prefixes of messages. CBC has very high diffusion, since the information from one block is spread through the successive blocks. It is also immune from the substitution attack described above. One negative aspect of CBC is that a single bit error propagates throughout multiple blocks and can render the entire message undecipherable.