Computes Ackermann's function, A(x, y), for x = 3 and y = N. This function is a simple example of a total function that is computable but not primitive recursive. The function f(x) = A(x, x) grows much faster than polynomials or exponentials. A(x, y) is defined as:
1. If x = 0 then A(x, y) = y + 1
2. If y = 0 then A(x, y) = A(x-1, 1)
3. Otherwise, A(x, y) = A(x-1, A(x, y-1))
Computing A(3, k) = 2(k+3) - 3 requires at least 4(k+1) function calls, and reaches a recursive depth of 2(k+3) -1. Thus computation of it stresses your compiler's ability to do deep recursion efficiently. In particular, it tests your code generation for function calls. If you happened to implement tail-call elimination you will see a very large performance gain.
Source: [ack.im ack.cpp Ack.java]
Input: N=10
Output: A(3,10) = 8189
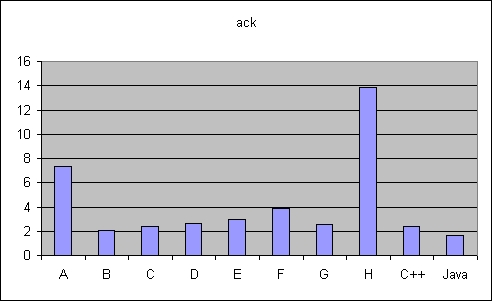
| Java | 1.63 |  |
| B | 2.03 | |
| C++ | 2.36 | |
| C | 2.38 | |
| G | 2.54 | |
| D | 2.62 | |
| E | 2.99 | |
| F | 3.89 | |
| A | 7.34 | |
| H | 13.88 |