In this handout, we provide static semantics for the Iota+ programming language, as a modification to the earlier Iota static semantics.
Class types and interface types will be represented in type equations as type N, where N is the name of the type. The actual information about the method signatures for these classes is stored in the environment A in the entry A[N]; this entry is itself an environment that maps method and field identifiers to their corresponding type signatures and types.We will assume a top-level environment, A0, that contains all of these entries.
An issue that was implicit in the Iota rules is how to convert type expressions to types. This issue becomes interesting with the introduction of class and interface types, because these types must be looked up in the current environment when encountered to determine whether they are valid types. In other words, an identifier N, used in a position where a type is expected, should not simply be converted to an internal representation as (type N); it must be validated against the current environment. We will write A ` T to indicate the judgement that T is a well-formed T in the environment A.
There are two judgments for type-checking in Iota+: the standard judgement present in Iota, A ` E : T, and a new judgment about subtype relationships, T1 <: T2. The first judgement says that the expression or statement E has the type T. The second judgment says that is a T1 is a subtype of T2. There are certain axioms that extend the power of these judgements. First of all, there is the fundamental subsumption rule that connects these two kinds of judgments:
| A ` E : T1 |
| T1 <: T2 |
| A ` E : T2 |
In addition, the subtyping relation is reflexive and transitive, so it is a pre-order:
T1 <: T2 |
||
T2 <: T3 |
||
T <: T |
T1 <: T3 |
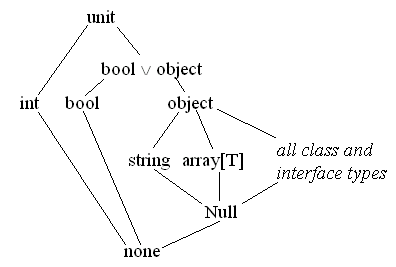
The types unit and none have associated subtyping
axioms: for all types T, T <: unit and none <: T. Also, the types Null and object
have pre-defined subtype relations: for all class and interface types N, type N
<: object and Null <: type N. Also, the types string and
array[T] are subtypes of object and supertypes of Null.
A figure showing these and other subtyping
relations is given below. Note that the types Null and none are
quite different, despite the similarity of their names. The type Null has
a single value, the constant null. The type none has no
values because it is the type of expressions that do not even return control to
their context.
Because of the new rule that none is considered a subtype of all other types, some of the earlier Iota rules are superfluous. For example, we no longer need the Iota rule that allowed a function body to have the type none even though the function was declared to have some particular type; subsumption takes care of this case automatically.
Finally, we have rules for inferring subtype relations among different object types:
| class N implements N' { ... } 2 A0 | interface N extends N' { ... } 2 A0 | |
|
type N <: type N' |
type N <: type N' |
Note that more indirect relationships in the subtype hierarchy are derived from the rule for transitivity.
The hierarchy of types induced by the subtype relation (it is, in fact, a lattice) described here is conveniently summarized by the following diagram:

Note that several of these types cannot be mentioned directly in an Iota+ program: unit, none, Null, and bool _ object. Unlike in Java, there is no subtype relation between two types array[T1] and array[T2] where T1 is not the same as T2.
The rules for existing Iota expressions remain the same, although they become richer because of the addition of the subsumption rule. However, various new expressions have been added to the language and rules for checking them are needed.
The type of the new expression this is looked up in the environment under the
special name this:
| ( this : T ) 2 A |
|
|
A `
this : T |
The type of the new expression null is always the special type Null:
for all environments A, A `
null : Null.
The type of the expression new N, where N is the name of a class, is type
N, but requires a check that the class N actually exists in the environment (which
guarantees that its declaration was valid):
| class N ... { ... } 2 A0 |
A ` new N : type N |
The type of a field access is looked up in the environment of the class:
| A ` E : type N |
| A[N] ` id : T |
| A ` E . id : T |
A method call is checked by ensuring that the types of each of the actual expressions supplied as arguments are the same as the declared types of the formal arguments. Note that this rule looks in the appropriate class environment to find the signature of the function named id.
| A ` E : type N |
| {id : T1 × T2 × ... × Tn! T} 2 A[N] |
| A ` Ei : Ti i 2 [1, n] |
A ` E . id ( E1,...,En ) : T |
Fields and methods of the pseudo-variable this may be accessed without
explicitly naming the object on which they are being invoked. Special rules are needed to
support these shorthands:
| this: type N 2 A | ||
| this: type N 2 A | {id : T1 × T2 × ... × Tn! T} Î A[N] | |
| A[N] ` id : T | A ` Ei : Ti i Î [1, n] | |
A ` id : T |
A ` id ( E1,...,En ) : T |
Finally, the cast expression has exactly the type it claims to (the
expression returns null if necessary to make this happen):
| A ` E : object |
| A ` T |
| T <: object |
A `
cast ( E, T ) :
T |
Some existing Iota expressions are changed slightly. The & and |
operators accept object types as arguments as well as booleans.
| A ` E1 : bool _ A ` E1 : object | A ` E1 : bool _ A ` E1 : object | |
| A ` E2 : bool _ A ` E2 : object | A ` E2 : bool _ A ` E2 : object | |
A ` E1 & E2 : bool |
A ` E1 | E2 : bool |
Another way to model this is by introducing a special union type bool _ object that sits above both bool and object in the type hierarchy: bool <: bool _ object and object <: bool _ object. The subsumption rule will automatically shift the type of an expression up to bool _ object when necessary. The operators that can accept either a boolean or an object are then typed as accepting values of type bool _ object. However, we are prevented by the type system from assigning an object directly into a boolean variable, which will help avoid programming errors.
| A ` E1 : bool _ object | A ` E1 : bool _ object | |||
| A ` E2 : bool _ object | A ` E2 : bool _ object | A ` E : bool _ object | ||
A ` E1 & E2 : bool |
A ` E1 | E2 : bool |
A ` !E : bool |
For == and !=, two values may be compared as
long as they have a common supertype that is not unit,
none, or
bool _ object.
| A ` E1 : T |
| A ` E2 : T |
| T is not unit or none or bool _ object |
A ` E1
== E2 : bool |
The rule for != is identical to the rule for ==,
and the rules for <= and >=
are the same as for < and >, but are extended
to allow comparisons of bool as well as int
and string.
Statement forms also are extended in Iota+. The subtype relation between unit, none and other types in the type system actually makes it easier to express rules about statements.
There is a new kind of assignment statement: an assignment to a field. We will treat assignment statements as if they were expressions for the purpose of type checking. This treatment allows multiple assignment to be checked conveniently without changing the previously existing rules for checking assignment, recalling that assignment associates to the right.
| A ` E1 : type N | A[this] : type N | |
| A[N] = class N ... { id : T } | A[N] = class N ... { id : T } | |
| A ` E2 : T | A ` E2 : T | |
A ` E1 . id = E2 ;
: T |
A ` id = E2 : T |
The new increment and decrement can be checked exactly as if they were assignments to an addition expression:
A ` E = E + 1
: T |
A ` E = E - 1
: T |
|
A ` E++
: T |
A ` E--
: T |
The if statement and while statement are augmented to allow their test expressions to be either of type bool or of type object. Because of the subsumption rule, a special rule is no longer needed in the case where the two arms return different types:
| A ` E : bool _ object | ||
| A ` E : bool _ object | A ` S1 : T | |
| A ` S : T | A ` S2 : T | |
A ` if ( E ) S :
unit |
A ` if ( E ) S1 else S2
: T |
A while statement always has the type unit, and requires
that its test expression has type bool or object. In
addition, a special entry is added to the environment under the keyword break.
When a break statement is encountered, this entry is checked for. If the
entry is not present, the break statement has occurred outside any containing
while statement and is therefore illegal. The type of a break statement is
none because, like a return statement, the statement does not transfer control to the containing context.
| A ` E : bool _ object | ||||
| A + { break : unit } ` S : T | A ` S : T | ( break : unit ) 2 A | ||
A ` while ( E ) S
: unit |
A ` while (true) S
: none |
A ` break
: none |
Note that a statement of the form while (true) S is given the
type none, exactly in Iota, but only if S does not execute any break
statements that would cause the while loop to terminate normally. This is
enforced in the rules by trying the type-checking of S twice; in practice, we want to try the none rule first since it subsumes the unit rule
when it is applicable.
A return statement is checked as before:
| A ` E : T | ||
| ( return : T ) 2 A | ||
| ( return : unit ) 2 A | T is not unit | |
A ` return :
none |
A ` return E : none |
Finally, the rule for checking blocks of statements is changed to prevent a statement with type none from making the subsequent statements unreachable:
|
A ` S1 : T1 |
A ` S1 : T1 |
|
| S1 is not a declaration |
S1 = id : T [ = E ] |
|
|
T1 is not none |
T1 is not none | |
| A ` ( S2 ; ... ; Sn ) : Tn | A + { id : T } ` ( S2 ... Sn ) : Tn | |
|
|
|
|
| A ` ( S1 ; ... ; Sn ) : Tn | A ` ( S1 ; ... ; Sn ) : Tn |
As in Iota, the goal of the type checker is to determine whether an entire module M is well-typed. This judgment will be written as ` M, where M is the text of the module. To check a module, we first construct an environment in which all of the module "uses" definitions and the components of the module themselves appear. This environment construction is performed by the function module-env, which must be extended to handle the new kinds of definitions found in Iota+. In Iota, the type checker effectively made two passes over the module; one to pick up the signatures of all the functions, and a second to actually check the function bodies. In Iota+, the first pass picks up the signatures of all the functions and the names of all the classes, interfaces, functions, and variables defined in the module. The second pass then checks all the method and function bodies. In the Iota semantics, the first pass was performed by the function module-env, which must be extended to handle the new kinds of definitions found in Iota+, including interface type declarations, class definitions, and constant definitions.
In addition, new rules for checking module definitions must be added to accommodate these kinds of definition kinds. With these additions, modules can be checked in exactly the same general way as before. As in Iota, a module must implement all of the values declared by its interface: module variables and functions. There is no necessity for a module to provide an implementation for interface types or for constant declarations, since the interface already states everything that one can know about these module components. When a module implements a component that is declared in its interface, the type of the component must conform to that declared in the interface. For variables, the two types must be equal. For functions, the type declared in the module must be a subtype of that declared in the interface. In other words, the types of arguments used in the actual definition of the function may be supertypes of those declared in the module interface, and the return type may be a subtype.
Class and interface definitions must also follow certain rules in order to avoid name clashes and type errors. A class or interface type may not define any members that have the same name as any supertype member, unless the member is a method and its signature conforms to that in the supertype in the usual contravariant/covariant manner. No class members may have the same name as any function, top-level variable, class or interface in the module, either, because otherwise there would be ambiguity about what that member meant within the body of the methods of the class. Interface members may have the same names as global identifiers because they are never introduced into scope automatically.
One problem that you may encounter in writing your compiler is that on the first pass it is not possible to check even the signatures of the class declarations that are entered into the environment, because the compiler will not necessarily know all of the types it needs to in order to understand the field and method signatures of the class. There are two ways of dealing with this problem, as described in lecture. One approach is to enter the class and interface type definitions into the symbol tables using un-interpreted type expressions (AST nodes). This approach requires that the appropriate environment always be carried around to resolve identifiers used in the AST trees representing types. The second approach is to add an additional pass over the symbol table that interprets all of the type expressions used in the class member signatures and replaces the symbol table entries with fully-resolved entries. The second approach is recommended, though both can be made to work.
Let F denotes a function declaration. An interface type declaration is legal if the signatures of all of its methods are conformant with those in its supertypes, if any:
| A ` conformant(Fi, A[N']) i21..n |
A ` interface N [
extends N' ] {
F1, ..., Fn } defn |
A method is conformant either if no method of that name exists in any supertype, or if a method of that name exists, but with the same number of arguments, where the arguments in the supertype method are subtypes of the arguments in the subtype method, and the return type in the supertype method is a supertype of the return type in the subtype method.
| :9i21..n
Fi
=
id(a'1
: T1,..., a'k : Tk) : T'r A ` conformant(id(ai : Ti) : Tr, A[N'']) i21..m |
A ` conformant(id(a1
: T1,..., am : Tm) : Tr, interface N' [
extends N'' ] { F1,...,Fn
}) |
| 9i21..m
Fi
= id(a'1 : T'1,..., a'm : T'm) : T'r T'i <: Ti i21..m Tr <: T'r |
A ` conformant(id(a1:T1,
..., am:Tm)
: Tr, interface N' [ extends N'' ] { F1,...,Fn
}) |
A class is checked similarly to an interface, in that method signatures must be checked for conformance. However, a class definition requires three additional kinds of checks: the members of the class may not conflict with anything in the environment, all supertype methods must be implemented by some method body, and the method bodies must be checked as well.
| A' = module-env(D1,...,Dn) A' + {this : type N} ` Di defn i21..n (Di = (F = E)) ) A ` conformant(F, A[N']) |
A ` class N [
implements N' ] { D1,...,Dn
} defn |
A method in a class is checked in much the same way as a function is. There is one difference: the environment is assumed to contain a binding from this to the type of the current class. Otherwise, the same rules can be used for type-checking methods as for type-checking functions.