Taking Big-Oh to the Formal
So what's with this Big-Oh notation? We have talked a lot in section about how to tell what the Big-Oh time complexity of an algorithm is from a hand-wavy, intuitive standpoint. Now, let's talk about formally defining Big-Oh.
Warning: The following are "Robin" definitions. Unfortunately, I don't have a Ph.D. and thus anything that I define isn't a formal definition.
Definition
A function f(n) is said to be O(g(n)) if there exists a constant c
and a point no such that
f(n) ≤ c*g(n) for all n ≥ no
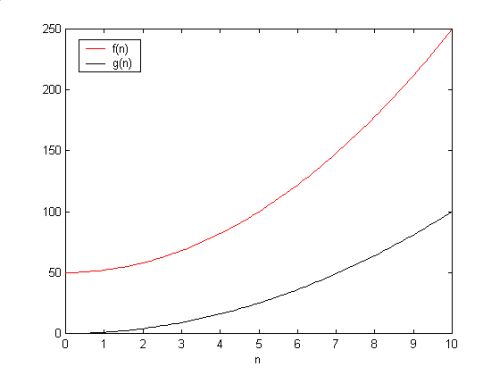
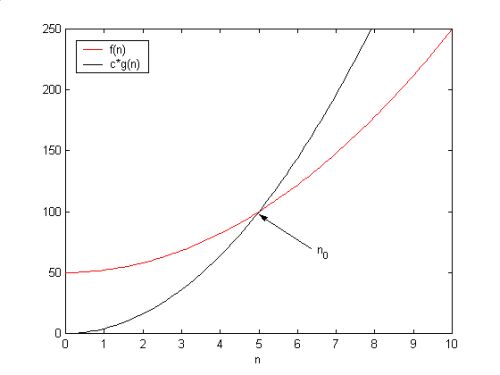
What the heck?!?! It looks a bit mathy, and if you aren't a math guy (or girl), then you may are probably confused. Let's draw a few pictures to try and see if we can understand the definition... Pictorially, let f(n) be the red line in the graph below, and let g(n) be the black line. At first, we take a look at the graphs, and they will not intersect in the first quadrant. What we do then is multiply g(n) by c and get the graph on the right. Now the graphs intersect. Notice that as n goes to infinity, f(n) is always less than c*g(n) after that intersection point. This x-coordinate of the intersection point is no. When this happens, it is safe to say that f(n) is O(g(n)).


Example
Let's try an example... We wish to prove the following:
3n + 8 = O(n)
Although this may seem a bit obvious, we are going to prove this formally. From the definition above, if 3n + 8 = O(n), then
3n + 8 ≤ c*n for all n ≥ n0
for some c and some n0. Let us manipulate the above equation in the following way...
3n + 8 ≤ c*n
(c - 3)n ≥ 8 (1)
Let us choose c = 11. Then, for all n ≥ 1, equation (1) holds true. Therefore, since we can find c and n0 such that equation (1) holds true, 3n + 8 = O(n).